
In our previous article, we learned about the Insertion Sort Algorithm. In Insertion Sort Algorithm, we have seen that in each iteration, we took an item from the unsorted portion, compare it with neighbour sorted item and it continued until the taken item got its right position. Accordingly, for placing an item in its right position, we need so many movements. For reducing this number of movement, the Shell Sort Algorithm comes into play.
Shell Sort Algorithm
The Shell Sort Algorithm is just a variation of the Insertion Sort Algorithm. But it does not require so many movements. In the first iteration, this algorithm takes an element to sorts by comparing it with the item far apart from the taken item. Then the position for taking the item to sort will be shifted to the right by one and it will be compared again with the item which is far apart. It will be continuing until the taking item’s position is less than the length of the collection.
In the second iteration, the gap will be reduced, and the rest of the tasks are the same as in the first iteration. For determining the gap, there are a number of ways (sequences) we can calculate the gap value. The gap value is also sometimes called interval. One most common sequence is Knuth’s Sequence. But another most common and easy sequence is Shell’s original sequence (N/2, N/4...1, where the N is the total number of items in the array) which is based on the array’s length. We are going to use this sequence during our example.
Let’s have an example:
For explaining the Shell Sort, let’s consider an array:

Here, the total number in the array is 7 (N = 7). If we divide the value of N by 2, we will get 3.5, but here the gap will be 3.
For the first iteration, here, the 0th item is 11, and this 11 will be compared with 4 (the difference between the position of 11 and 4 is 3). The 4 will be taken to put it in its correct position by comparing it with 11. Now, as 4 is smaller than 11, so 11 will be shifted to the place of 4, and finally, the 4 will be placed to the place of 11.
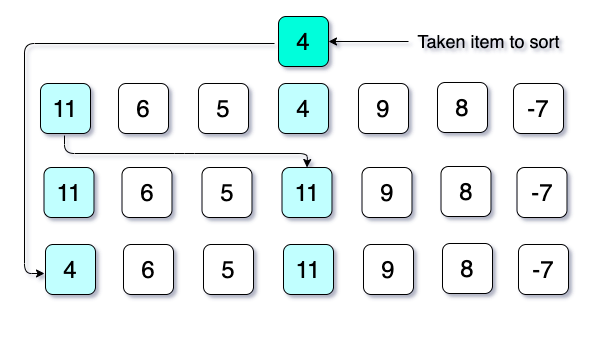
Now the position for taking the item will be increased by one. In this case, the item is 9, and it will be compared with 6 (as the gap is 3). As 9 is greater than 6, and before 6, we have only one value, but the gap value is 3. So, we cannot compare it with any other numbers. Now it is clear that they are in their correct position. And this process will be continuing until the last item on the list. Here is the illustration:
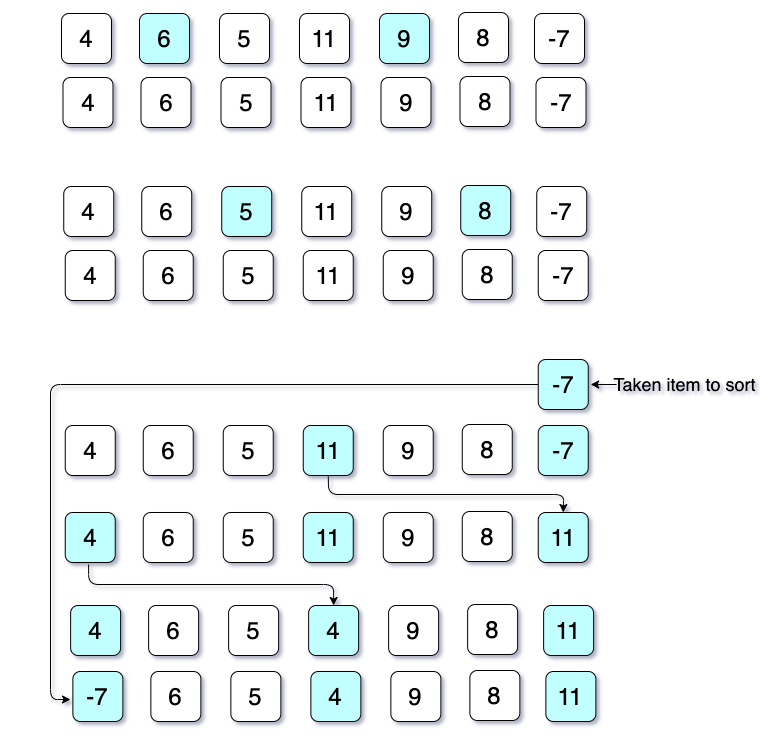
In the last portion, where -7 is taken to sort, first, we compare -7 with 11 and put 11 at the place of -7. Then, again we have at least three values at the left of 11, so we can compare -7 again with 4 (4 is the value with gap 3), and as -7 is less than 4, so 4 will put at the position of 11. Finally, as we don’t have any further value to compare, the taken value will be put at the position of 4.
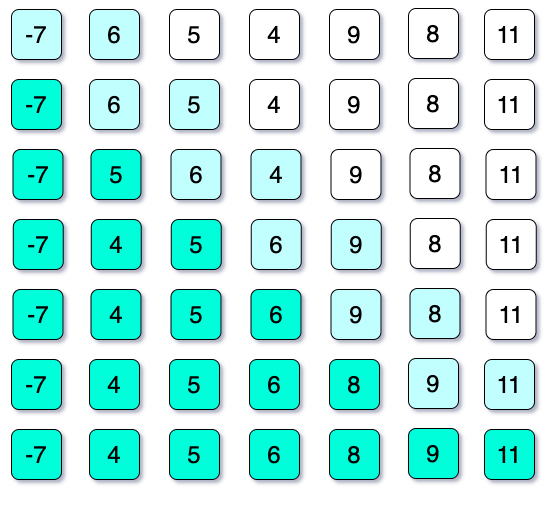
In the second iteration, we will divide 3 by 2 (or N/4, where N = 7). Then we will get the new gap value 1. As the value of N is odd, we always take just the integer value. If the value of N is an even number, then we will take the exact value. As the gap value is 1, then this iteration will work as Insertion Sort. For the Shell Sort Algorithm, always the last iteration of the Shell Sort is similar to the Insertion Sort.
Let’s have an implementation using Java:
In our above implementation, we are seeing that the first loop is iterating based on the gap. And for each iteration, the gap is being divided by 2 which you have got the explanation above.
Inside the second loop, we are taking the item in newElement to sort, and in each iteration, we are shifting the taking point to the right. In the while loop, we are comparing the taken item’s position is greater than the gap or not, and we are also comparing the taken item with an item with the gap. If these two conditions are filled, then the item with the gap will be placed in the taken item’s position. Then, this program will shift the taken item’s position and the gap to the left. If the while loop's conditions are not filled, it means, either the newElement is larger, or in the left, we don’t have enough gap. So, the correct position of the taken item to sort (newElement) is j (array[j] = newElement).
Time Complexity of Shell Sort Algorithm
For Shell Sort, the time complexity is always O(n2) or less the O(n2). The complexity will be O(n*log n) for the already sorted collection. And it the best-case scenario. But the average case time complexity is O(n*log n), which is around O(n1.25).



