Merge Sort Algorithm: Understanding Its Process, Efficiency, and Applications

In this article, we are going to learn about Merge Sort Algorithm which is a very popular sorting algorithm based on Recursive Algorithm. This algorithm works on the Divide and Conquer principle. Let’s begins the main lesson.

Before diving into the main lesson, it would be better if we have a basic concept about the Divide and Conquer algorithm as the Merge Sort Algorithm works on the principle of the Divide and Conquer algorithm.

What is Divide and Conquer Technic?

For solving a large problem, we sometimes break the problems into smaller sub-problems for making easy the solving procedure. After solving each sub-problems, we combine all the solutions into a single solution for getting our desired output. This is called Divide and Conquer technic or algorithm.

Divide
For instance, let’s think of an array, which we will sort using Merge Sort Algorithm. In this Merge Sort Algorithm, we will Divide the array into sub-array. It will be continuing recursively (sub-arrays will also be divided) until each sub-arrays are of size 1. Let’s have a look at the illustration below:

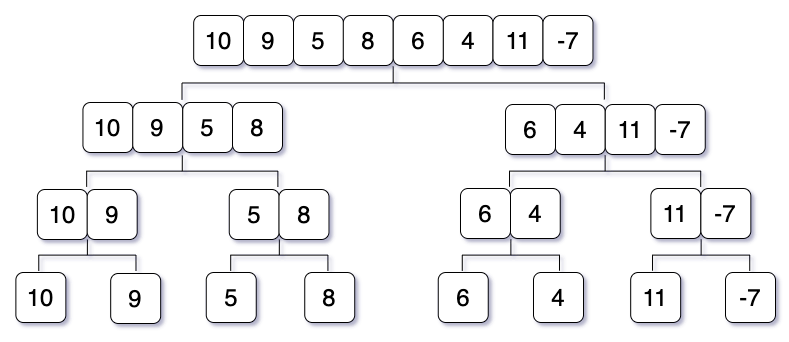
Conquer
After completing the dividing steps, we will get several sub-arrays and at the end, each array will have size 1. In this Conquer step, the last smaller sub-arrays will be sorted and formulate first, and this step will be continuing until the complete array is formulated. Here is the graphical illustration.

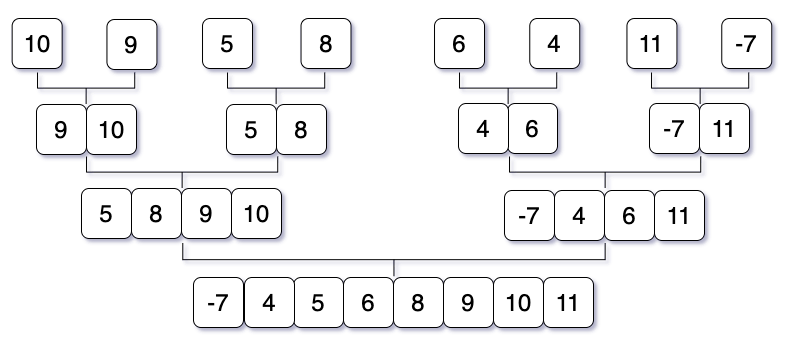
Let’s dive into the Merge Sort Algorithm

As we mentioned earlier, the Merge Sort Algorithm works on the principle of the Divide and Conquer technic, this algorithm divides the array recursively into two halves until the last sub-arrays sizes are 1. That does mean, the starting point and ending point of a sub-array will be equal.
So, let’s have a look at the pseudo code of this explanation:

mergeSortAlgo(array, startingPoint, endingPoint)
    if(startingPoint >= endingPoint)   //dividing is done
        return
    mid = (startingPoin + endingPoint) / 2
    mergeSortAlgo(array, startingPoin, mid)       //work with left halve of the array
    mergeSortAlgo(array, mid + 1, endingPoint)    //work with right halve of the array
    merge(array,startingPoint, mid, endingPoint)  //merge sorted sub-arrays to formulate final sorted array

Here, for dividing the array, we need to call the mergeSortAlgo method. After entering the method, if the array (or sub-array) size is 1, this method execution will be stopped. If the array (or sub-array) size is more than 1, then the array (or sub-array) will be divided again. As it is following the recursive algorithm, it will be continuing until the sub-arrays sizes are 1.

Merge Method

After this division, the merge method will come into the front. And this method takes the sub-arrays to merge in a sorted manner.
For explaining the merging steps, the sub-arrays are:

Here, each item are considered as a single element’s array. Now, sub-array {10} and {9} will be merged in a sorted manner. After merging into a single array, it will look like this: {9, 10}.
Again, {5} and {8} will be merged into {5, 8}. Then, {9, 10} and {5,8} will merge.

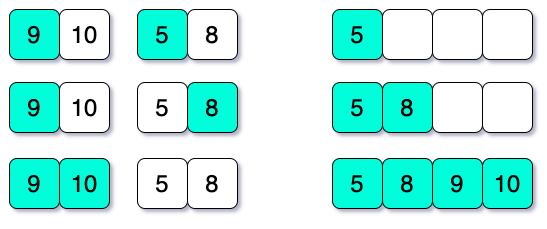
In the last portion of the picture, we have seen that there are no remaining elements in the right side’s sub-array. But, we know both the arrays are sorted. So, we can simply put the remaining elements of the left side array into the sorted array.
Following the same procedure, now we will work with the sub-arrays {6}, {4}, {11} and {-7}. If we merge {6} and {4}, the merged sorted array will be looked like this: {4, 6}. And if we merge {11} and {-7}, then the merged sort will be {-7, 11}.

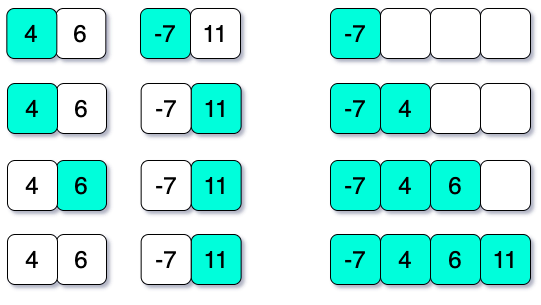
Now, we have two sorted sub-arrays and we need to merge these into a single array. Two sorted sub-arrays are {5, 8, 9, 10} and {-7, 4, 6, 11}.
Let’s illustrate it with a picture:

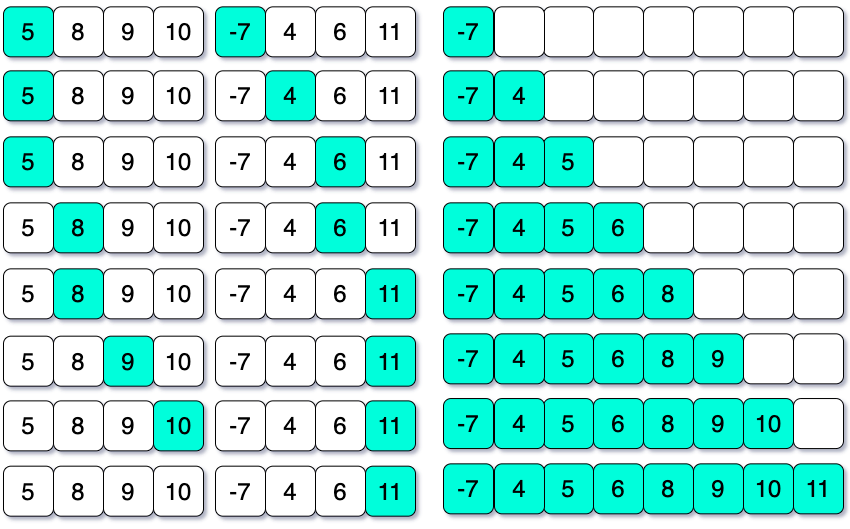
Finally we are getting the sorted array: {-7, 4, 5, 6, 8, 9, 10, 11}.

Implementation of Merge Sort Algorithm using Java