
The Insertion Sort Algorithm
The Insertion Sort Algorithm is a very simple sorting algorithm. It proceeds by traverse the list and placed a single item from the list in a sorted position in each iteration. In each iteration, an item is taken from the unsorted portion and placed it in its appropriate position by comparing it with sorted items. In this algorithm, the first item is always considered as sorted. Therefore, the first comparison happens between 2nd(first unsorted item) and and 1st (sorted element) elements.
Working Steps of Insertion Sort Algorithm
For explaining the working steps, let’s consider an unsorted list of integers:

According to the Insertion Sort Algorithm roles, first, we consider the item of position 0 (in this list, 6 is the first item) is sorted. So, here the unsorted portion is from position 1 to position 4. Then the first unsorted item is 5 (position is 1).
First Iteration
In the first iteration, we will take 5 to place it in its appropriate position by comparing sorted item(s) (here only 6). So, if we compare 5 (position 1) with 6 (position 0), we can see the value of position 1 is smaller than the value of position 0. Therefore, the value of position 0 will be shifted to right for making a room for the taken item (5). Let’s have a graphical illustration of this first iteration:
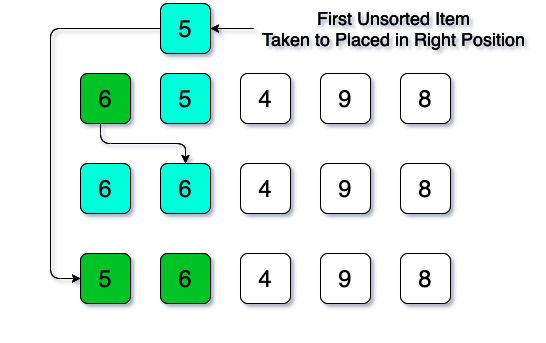
Now until the position 1 is the sorted portion of the list.
Second Iteration
For the second iteration, position 2 (value is 4) is the first unsorted item. So, this the item now we are taking to place it in its correct position. First, we compare 4 with 6 and 4 is smaller than 6. So, 6 will be shifted to right to make room for 4. Again 4 will be compared with 5 and here, 4 is also smaller. So, 5 will be shifted to right to make room for 4. Let’s illustrate it with a picture.
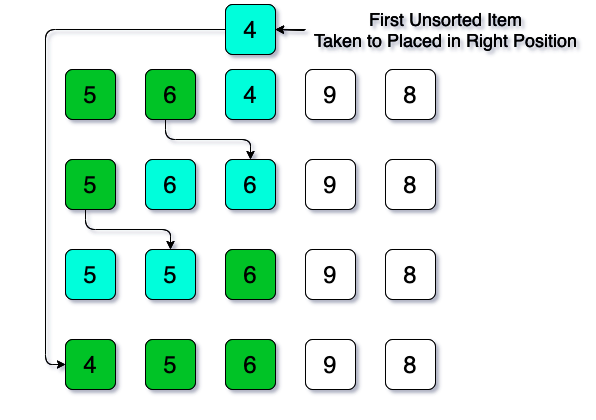
From position 0 to position 2, the portion of the list is sorted and the rest of the list is unsorted.
Third iteration
For the third iteration, the first unsorted item’s position is 3 (value is 9).
Now, if we take the first unsorted item (9) to place it in its correct position, the illustration would be like below:
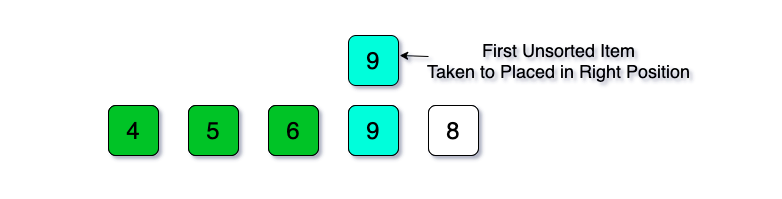
Here, we have seen that the taken item to put in the correct position is larger than the largest item of the sorted portion. It does mean that it is placed in its correct position. So we don’t need to compare it with all the sorted items. So from the position 0 to position 3, the items are sorted.
Fourth Iteration
For the fourth and final iteration, the first unsorted item’s position is 4 (value is 8) and now we need to put it in the right position. Here the depiction is looked like below:
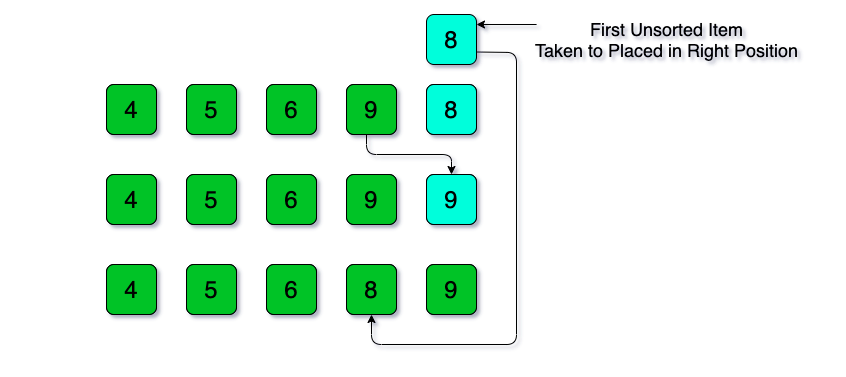
In the above picture, 8 has been taken to put it in its correct position. Then it is compared with the last item of the sorted list and found it as smaller. Then the last item of the sorted portion is shifted to right by one to make a room for the taken item. Again we compare the taken item (8) with the previous item of the last sorted item (6) and found the taken item as larger. So we don’t need to do further comparisons. Finally, the taken item will be placed in the room made by shifting the last sorted item to right.
Implementation of Insertion Sort using Java
Now we know how the Insertion Sort Algorithm works. So let’s have a look at the realtime implementation of this algorithm using Java programming language:
In the above program, we use 2 for loops. The first for loop initiate from 1. Because in this algorithm, we consider the first item as sorted. This loop will continue until the last item (firstUnsortedItem < array.length). In each iteration, we have taken the first unsorted item to placed it in its correct position. Before going to the second loop (inner loop), we have taken this item named takenElement. And the inner loop starts from the first unsorted item (i = firstUnsortedItem), and compare this unsorted item with the previous item (array[i - 1] > takenElement). This loop is iterating from right to left. Therefore this loop will continue if the value of i is greater than 0 and taken item is smaller than the value of i - 1 position (i > 0 && array[i - 1] > takenElement).
If these two conditions (i > 0 && array[i - 1] > takenElement) are satisfied, then the value of i - 1 will be shifted to right (array[i] = array[i - 1]). When these two conditions are not satisfied, the value of takenElement will be putted in the i number position (array[i] = takenElement) (when we check the conditions, the value of i is decreased by one).
If we think about the efficiency of this algorithm, we can say not so good. This algorithm is used basically when the number of elements is small. As we are using 2 loops, it is clear that the time complexity is O(n2) which similar to the Bubble Sort Algorithm.



