What is Big-O Notation
All the time, we write code, we have to think about how efficient the solution is. Because, in computer programming, we often have different ways to solve a single problem. For example, for sorting items, we can use merge sort, insertion sort, bubble sort, and so on. All these algorithms have some pros and cons. When we think about choosing the best algorithm, then the Big-O Notation comes into play.
For solving a problem, programmers always try to choose the most efficient algorithm. There are two things the efficiency of an algorithm depends on. One is time complexity and another one is memory or space complexity. Nowadays, memory is very cheap. Consequently, programmers often do not think about it. So, for making an algorithm efficient, time complexity is the main concern. When we compare two algorithms to find out the better one, the main issue where our first glance goes is the time complexity. And for measuring the time complexity, we have to know what the Big-O Notation is.
Big-O notation helps programmers to measure the scalability of an algorithm. It indicates the maximum number of operations taken by an algorithm for giving output based on how much data the program has to work on. In simple words, Big-O notation describes the relationship between steps required to execute the algorithm and input to the algorithm. This relationship shows the time efficiency or time complexity.
A computer program is just a list of steps of instructions on how the computer should go for solving a problem. And in short words, this is called an Algorithm. Here the Big-O notation defines how fast an algorithm is and lets us compare the program with others by showing the relationship between input and steps to execute the algorithms. For instance, if the relationship between the inputs to the algorithm and steps to execute the algorithm is linear, the Big-O notation will be O(n). And for the quadratic relationship between input and steps, the Big-O notation will be O(n²).
Let’s have a look on two examples below:
Example 1:
Example 2:
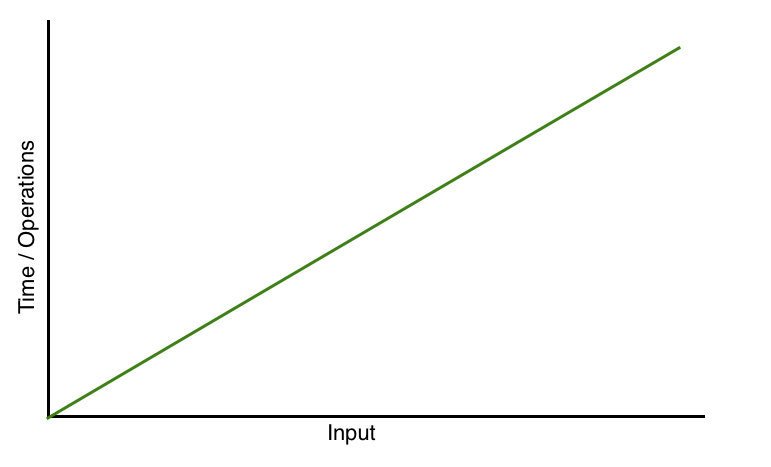
The tasks of both methods are the same. But in the first example all steps for solving the problem will be executed n times. If the value of n is 10, the steps will be executed 10 times and if the value of n is 10 million, then all steps will be executed 10 million times. Here the input and steps are increasing linearly. As a result, the growth rate of the time complexity is linear. So, here the Big-O notation is O(n). The graph of the efficiency of the algorithm used in example 1 looks like below:
In the second example, the steps are executed only for once. The execution time is not dependent on the input. Whatever the value of n, the steps will be executed just for once. And it is constant. So, here the growth rate of the time complexity is constant. And here the Big-O notation is n(1). The algorithm efficiency graph of the second method looks like below:
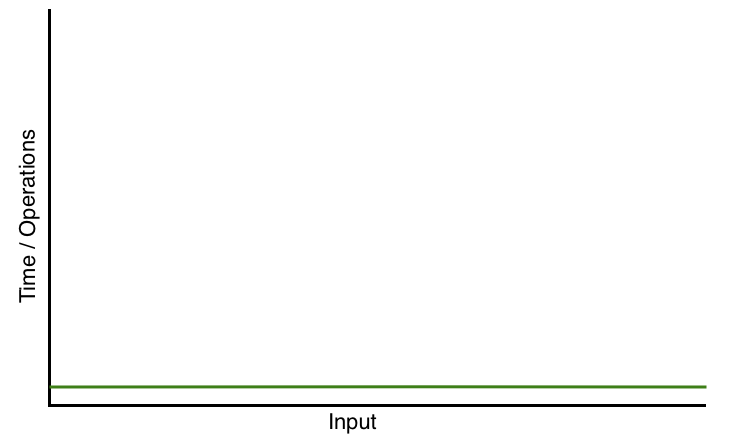
The time complexity for the first example is O(n) and for the second example, it is O(1). So, it is very clear that the second solution (or steps to be executed or algorithm) is the most efficient solution.
For the cases of nested For Loops, the growth rate will be quadratic. And it will be denoted by O(n²).
Let’s have an example:
This method is used for finding duplicate items between two lists.
Here, the solution has used a nested loop. If the elements1 and elements2 each contain 100 items, then the total loop execution time will be 100*100. If the elements1 contains n number of items and elements2 contains n number of items then the loop will be executed n*n or n² times. So the time complexity of the solution will be O(n²).
The graph of quadratic growth rate is below:
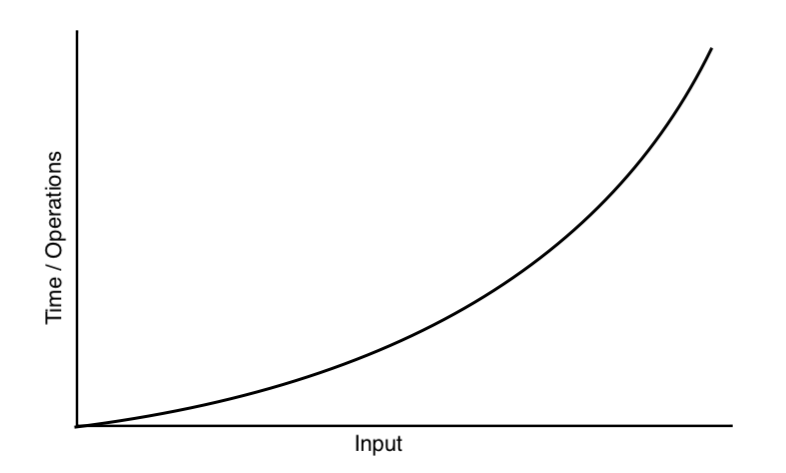
Big-O is used for the approximate worst-case performance of solving a problem
Let’s have a look on a solution:
This method is used for checking an item whether it is in the list or not. The above solution tells us the Big-O notation is O(n). It means if we want to check the item (itemToCheck) in the list n, in the worst-case, we will have to check every single item (using Simple Search algorithm). But when we will run the simple search algorithm, we may find the item at the very beginning of the list n, maybe in the first element of the list is matched with the itemToCheck. In that case, the solution above will return true and the rest of the program will not run. For this input (itemToCheck, you checked in the above solution) the Big-O notation may O(1). This is the best-case scenario. But all the time, Big-O notation considers the worst-case scenario, which is O(n) for the solution above.
The Big-O notation is not for measuring time an algorithm will run. Because the time of an algorithm depends on many things. Instead of showing the time, it shows the number of operations an algorithm will perform. And this number of operations tells the programmer how fast an algorithm is and helps the programmer to compare it with others.
